
Популярные задачи:
Пирамидальная сортировка
Пирамидальная сортировка в некотором роде является модификацией такого подхода, как сортировка выбором, с тем лишь отличием, что минимальный(или максимальный) элемент из неотсортированной последовательности выбирается не за O(n) операций, а за O(log n). Соответственно и производительность такого метода будет не ~ O(n2), а O(n*log n), т.е. наиболее быстрая для сортировки.
Естественно, без дополнительных манипуляций с неотсортированной последовательностью мы не добьемся выбора из нее максимального(в пирамидальной сортировке выбирается максимальный, поэтому дальше будем это всегда предполагать) элемента за O(log n). Точнее, для такого быстрого выбора из этой неотсортированной последовательности строится некоторая структура. И вот именно суть метода пирамидальной сортировки и состоит в построении такой структуры, называемой соответственно "пирамидой".
Суть метода
Теперь весь метод в целом. Вначале имеем исходную нашу неотсортированную последовательность. Из нее строится вышеупомянутая структура данных - пирамида. Пирамида обладает тем свойством, что в ее вершине - находится максимальный элемент. Кроме того вершина - это элемент в структуре пирамиды с начальным индексом. Поэтому чтобы выбрать из пирамиды максимальный элемент - не нужно делать вообще ничего - нужно просто взять этот начальный элемент стуктуры пирамиды.
Пирамида построена, далее можно начинать основные итерации сортировки. На каждой итерации:
1. Вынимаем вершину пирамиды
2. На ее место вставляем последний в пирамиде элемент
3. "Просеиваем" этот элемент сквозь пирамиду.
И так до последней итерации на которой из всей пирамиды останется только вершина, которую мы и вставим в конец нашей полученной отсортированной последовательности.
Просеивание
Неясным остался момент "просеивания" элемента сквозь пирамиду. Под этим подразумевается восстановление баланса пирамиды. После того как мы ставим последний элемент на вершину - пирамида теряет свои свойства, становится "разбалансированной". Поэтому дальше нужно этот элемент поставить в соответсвующее ему место, а на вершину восстановить максимальный элемент.
Так работает пирамидальная сортировка: перед сортировкой строится пирамида, на каждой итерации мы вынимаем из нее максимальный элемент и ставим в свою отсортированную последовательность, и далее восстанавливаем баланс пирамиды.
Структура пирамиды
Теперь рассмотрим наконец что же представляет из себя эта пирамида. Это бинарное дерево, в котором каждый элемент меньше либо равен его родителю.
Например, имеем исходную последовательность:
x = [22, 100, 44, 15, 2, 36, 53, 23, 82, 5]
Пирамида для нее будет выглядеть как:
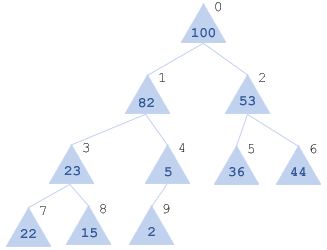
Хранить пирамиду удобно в виде массиве. Нумерацию элементов пирамиды определяем просто: проходимся сверху вниз, слева направо по каждому элементу и нумеруем его. В итоге получим то, что изображено на рисунке(цифры черным цветом - искомые индексы).
Т.о. получим x[0] - вершина пирамиды, а левый и правый потомки каждого элемента x[i] будут соответственно: x[2*i+1] и x[2*i+2] и основное свойство пирамиды тогда можно записать как:
x[i] >= max( x[2*i+1], x[2*i+2] )
Построение пирамиды
Исходный массив делится пополам, вторая его половина уже принимается за пирамиду. Затем последовательно берутся элементы из первой половины и добавляются в пирамиду.
Может возникнуть вопрос: с чего это вдруг мы сразу пол-массива считаем за пирамиду, а не строим ее шаг за шагом начиная с последнего элемента, добавляя туда потом предпоследний и т.д. до первого элемента? Дело все в том, что для второй половины нашего исходного массива основное свойство пирамиды - выполняется автоматически. Вернее, оно не нарушается, поскольку для элементов второй половины просто уже не будет потомков!!! Действительно: потомки для всех x[i], где i = n/2..n будут соответственно x[n+1]...x[2*n+2], т.е. такие, которых в нашем массиве уже нет. А поэтому нет смысла для элементов второй половины строить пирамиду последовательно добавляя каждый элемент, т.к. в алгоритме текущий добавляемый элемент просто будет не с чем сравнивать, сыновей-то с такими индексами - просто нет!
Так что спокойно принимаем вторую половину нашей последовательности как пирамиду и приступаем к следующему этапу построения - добавлению элементов.
Чтобы добавить элемент в пирамиду - нужно поменять его с наибольшим ребенком, если последний превосходит добавляемый элемент. Затем тоже самое по отношению уже к новым его детям. Т.о. чтобы добавить в пирамиду новый элемент x[i], нужно:
- Добавить элемент x[i] слева к массиву уже имеющейся пирамиды
- Найти максимального из его сыновей: maxChild = max( x[2*i+1], x[2*i+2] )
- Если x[i] >= maxChild - завершение процедуры, элемент занимает положенное ему место, добавление завершено, иначе - шаг 4.
- maxChild > x[i] - поменять их местами(т.е. поменять местами x[i] и его большего ребенка).
Перейти к шагу 2, учитывая новое положение добавляемого элемента.
При этом, как можно догадаться - просеивание, о котором велась речь выше - это тоже добавление, поскольку после удаления максимального элемента, т.е. вершины пирамиды, мы ставим на его место последний элемент, а это по-сути - опять же добавление элемента в пирамиду. Поэтому для просеивания нам не нужно писать еще одну функцию, мы просто вызываем добавление по-отношению к этому новому элементу.
В итоге имеем лишь единственную процедуру, которую можно назвать общим понятием для этих двух действий - назовем ее "восстановлением баланса пирамиды".
Выглядеть она будет примерно следующим образом:
На каждом шаге этого цикла мы продвигаемся на 2*ij позиций вперед по направлению к концу пирамиды(массивы), где j - номер итерации цикла. Т.о. данная процедура займет порядка ~ O(log n) времени.
Имея такую функцию процедура построения пирамиды займет...1(!!) строчку:
В итоге получаем производительность процедуры построения порядка ~O(n*log n).
Пример. Построим пирамиду для последовательности x = [22, 100, 44, 15, 2, 36, 53, 23, 82, 5].
Делим пополам: 22, 100, 44, 15, 2 | 36, 53, 23, 82, 5. То что справа уже пирамида, слева - то, что будет просеиваться через нее. Т.о. получим(темные элементы - пирамида, светлые - что предстоит просеивать):
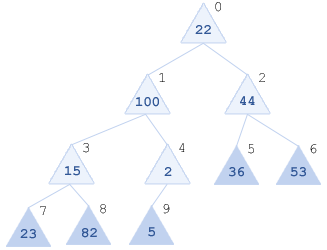
- Шаг. Просеиваем x[4] = 2 через пирамиду [36, 53, 23, 82, 5]
Дети этого элемента, вернее только один: x[9] = 5. 5>2 => меняем местами x[4], x[9].
Далее дети x[9] - нет уже => итерация завершена, новая пирамида: [5, 36, 53, 23, 82, 2]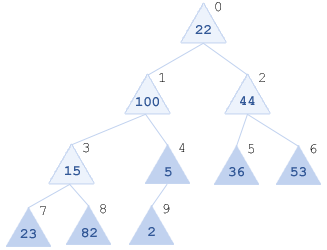
- Шаг. Просеиваем x[3]=15 через [5, 36, 53, 23, 82, 2].
Дети: x[7]=23, x[8]=82. x[8] - наибольший. Т.к. x[8]=82 > x[3]=15 => Обмениваем x[3],x[8].
У x[8] - детей уже нет => итерация завершена, новая пирамида: [82, 5, 36, 53, 23, 15, 2]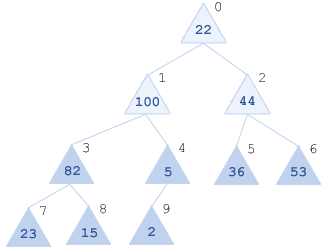
- Шаг. Просеиваем x[2]=44 через [82, 5, 36, 53, 23, 15, 2].
Здесь, аналогично, получаем: обмен x[2],x[6], новая пирамида [53, 82, 5, 36, 44, 23, 15, 2]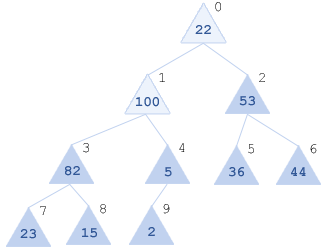
- Шаг. Просеиваем x[1]=100 через [53, 82, 5, 36, 44, 23, 15, 2].
x[1] больше максимального(x[3]=82) своего ребенка. Итерация завершается без обменов.
Новая пирамида: [100, 53, 82, 5, 36, 44, 23, 15, 2]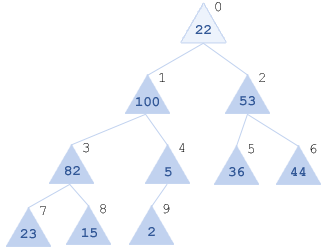
- Шаг. Просеиваем x[0]=22 через [100, 53, 82, 5, 36, 44, 23, 15, 2].
Наибольший ребенок x[1]=100 > x[0] => обмениваем x[0],x[1].
Получаем [100, 22, 53, 82, 5, 36, 44, 23, 15, 2]: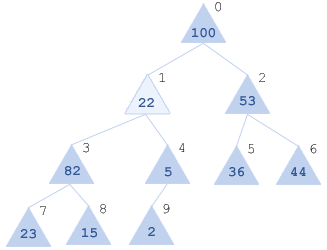
Далее согласно алгоритму, смотрим детей уже для нового x[1] = 22: x[3]=82,x[4]=5.
Максимальный x[3]=82 > x[1]=22 => меням x[1],x[3].
Получили [100, 82, 53, 22, 5, 36, 44, 23, 15, 2]: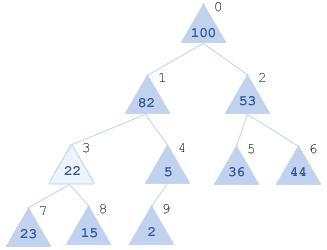

Опять смотрим детей уже для нового x[3]=22: x[7]=23, x[8]=15.
Максимальный x[7]>x[3] => обмен x[7],x[3].
Получили [100, 82, 53, 23, 5, 36, 44, 22, 15, 2]:
У x[7] - детей уже нет => итерация завершена.
В результате получили построенную пирамиду. Особо следует обратить внимание на Шаг 5, в котором вершина 22 просеилась в 3 прохода до самого последнего уровня, в отличие от других шагов, где имела место максимум 1 перестановка.
Сортировка
После построения пирамиды запускается процедура сортировки.
Из пирамиды изымается вершина, ставится вначале будущей отсортированной последовательности. На ее место помещается конечный элемент пирамиды и просеивается через нее, занимая положенное ему место. В итоге на вершину восходит снова максимальный элемент. На втором шаге снова вершина снова перемещается в конечную последовательность и т.д. до тех пор пока вся пирамида не кончится.
Этот алгоритм уже будет сортировать все как нам надо и также быстро, но будет использовать дополнительную память под новую последовательность. Этого можно избежать путем введения в своем роде "хака" в пирамиду. Что если мы на каждом шаге вершину будем не изымать, а просто обменивать с конечным элементом пирамиды? Естественно с тем конечным элементом, который еще обменивался с вершиной, т.е. чтобы снова не обменивать уже раз поставленные вершины на предыдущих шагах в конец? В этом случае наша пирамида будет просто постепенно вырождаться в отсортированную последовательность, которая нам и нужна.
Алгоритм:
- Устанавливаем границы пирамиды c 0 по n-1, т.е. на данном этапе вся пирамида x[0..n-1]
А вершина(heap) = 0 и конец(tail) = n-1 - Меняем x[heap] и x[tail]
- Корректируем tail = tail - 1
- Просеиваем новую вершину x[0] через пирамиду x[1..tail].
- Если tail = 1, то конец сортировки, иначе - п.2.
Для нашей построенной в предыдущем примере пирамиды, получим:
- Обмен x[0]=100, x[9]=2; просеивание x[0]=2 через [82 53 23 5 36 44 22 15]
Получим: [82 23 53 22 5 36 44 2 15 100]*. - Обмен x[0]=82 и x[8]=15, просеивание x[0]=15 через [23 53 22 5 36 44 2]
Получим: [53 23 44 22 5 36 15 2 82 100]* - Обмен x[0]=53 и x[7]=2, просеивание x[0]=53 через [23 44 22 5 36 15]
Получим: [44 23 36 22 5 2 15 53 82 100]* - Обмен x[0]=44 и x[6]=15, просеивание x[0]=44 через [23 36 22 5 2]
Получим: [36 23 15 22 5 2 44 53 82 100]* - Обмен x[0]=36 и x[5]=2, просеивание x[0]=2 через [23 15 22 5]
Получим: [23 22 15 2 5 36 44 53 82 100]* - Обмен x[0]=23 и x[4]=5, просеивание x[0]=5 через [23 15 2]
Получим: [22 5 15 2 23 36 44 53 82 100]* - Обмен x[0]=22 и x[3]=2, просеивание x[0]=2 через [5 15]
Получим: [15 5 2 22 23 36 44 53 82 100]* - Обмен x[0]=15 и x[2]=2, просеивание x[0]=2 через [5]. В данном случае все просеивание сведется к обмену x[0]=2 и x[1]=5.
Получим: [5 2 15 22 23 36 44 53 82 100]* - Обмен x[0]=2 и x[1]=5. Просеивание делать уже не имеет смысла. Однако если в конкретной реализации данного алгоритма оно запускается для такого случая - то процедура просеивания должна отличать такую ситуации и не делать никаких перестановок.
*Серым выделены элементы, которые как-бы изымаются из структуры пирамиды и представляют собой поэтапно формирующуюся искомую отсортированную последовательность. Они остаются в пирамиде просто для того, чтобы не расходовать доп. памяти на их новое хранение. Под пирамидой поэтому уже подразумевается последовательсность без этих серых элементов.
В результате получили искомую сортировку: x=[2 5 15 22 23 36 44 53 82 100], что и требовалось.
Псевдокод будет иметь вид:
Построение процедуры как уже отмечено выше занимает максимум ~O(n*log n) времени. Описанная фаза сортировки - максимум тоже ~O(n*log n). С среднем ~O(n/2 * log n) конечно. В итоге получаем метод, который сортирует за ~O(n*log n) времени и не использует дополнительной памяти.
Следует отметить, что если сравнивать с другой сортировкой порядка ~O(n*log n) такой как быстрая сортировка - то вторая выигрывает по производительности, но при этом как известно расходует намного больше памяти.
Реализации:
C++(1) +добавить1) Пирамидальная сортировка на C++, code #29[автор:this]


