Циклический сдвиг массива или строки - 3 уникальных алгоритма

• Вступление
• Алгоритм #1: последовательный обмен
• Алгоритм #2: перестановка блоков
• Алгоритм #3: переворотами
• Все реализации

Вступление

Циклический сдвиг массива влево - довольно понятная задача когда внутри массива из n элементов нужно взять кусок начиная с i-ой позиции (и до конца) и сдвинуть его в начало массива.
Например, если n=8, a i=3,  то массив символов "abcdefgh" должен будет превратиться в "defghabc". Дело в том, что алгоритм решения такой казалось бы ничем не выдающейся задачки играет большую роль, например, во всяческих различного рода текстовых редакторах, в каждом из которых сейчас уже обязательно присутствует такая возможность, как выделение мышкой текста и последующего его перемещения как есть в любое другое место редактируемого файла.

И вот если использовать очевидное решение в лоб: использовать n-элементный вспомогательный массив и сделав n шагов завершить всю перестановку - мы натыкаемся на дополнительный расход памяти, пропорционально растущий от объема этого выделенного, перемещаемого текста. Представьте себе, если выделяется текст большого объема, например, в миллион символов и перемещается. В этом случае весь этот миллион символов(байт) - а это уже мегабайт, будет занимать ценное место в оперативной памяти.

Поэтому было бы неплохо найти решение, которое осуществляло бы эту перестановку без дополнительного расхода памяти, по-крайней мере, чтобы этот расход не рос пропорционально объему сдвигаемого фрагмента.

И такое решение существует, а точнее даже целых 3 интересных и проверенных опытом алгоритма, которые позволяют обойтись лишь несколькими дополнительными переменными и завершить весь сдвиг не за n шагов, а всего лишь за время, пропорциональное n.

По книге Джона Бентли:
"Жемчужины программирования"

"... В некоторых языках программирования операция циклическо­го сдвига является элементарной (то есть выполняется одним оператором). Для нас важно, что циклический сдвиг соответствует обмену соседних блоков памяти разного размера: при перемещении фрагмента текста с помощью мыши из одного места файла в другое осуществляется именно эта операция. Ограничения по времени и объему памяти существенны для многих подобных приложений.

Можно попытаться решить задачу, копируя первые i элементов массива х во временный массив, сдвигая оставшиеся n-i элементов влево на i позиций, а затем копируя данные из временного массива обратно в основной массив на последние i позиций. Однако данная схема использует i дополнительных переменных, что требует дополнительной памяти. Другой подход заключается в том, чтобы определить функцию, сдвигающую массив влево на один элемент (за время, пропорциональное n), а потом вызывать ее i раз, но такой алгоритм будет отнимать слишком много времени.

Алгоритм #1: последовательный обмен

Решение проблемы с указанными ограничениями на использование ресурсов потребует написать более сложный алгоритм циклического сдвига массива.
Одним из вариантов решения будет введение дополнительной переменной. Элемент х[0] помещается во временную переменную t, затем x[i] помещается в x[0],x[2*i] — в х[1] и так далее (перебираются все элементы массива х с индексом по модулю n), пока мы не возвращаемся к элементу х [0], вместо которого записывается содержимое переменной t, после чего процесс завершается. Если i = 3, а n = 12, этот этап проходит следующим образом (рис. 2.2):

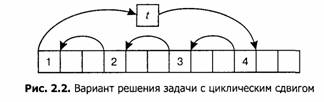
Если при этом не были переставлены все имеющиеся элементы, процедура повторяется, начиная с х[1] и так далее, до достижения конечного результата:

/* Сдвигаем массив x[0..n]
 * на rotdist позиций влево
 */
 
 
/* gcd - наибольший общий делитель
 * между n и rotdist
 */
for i = 0 to gcd
  t = x[i]
  j = i
  while
    k = j + rotdist
 
    if k >= n
      k -= n
 
    if k == i
      break
 
    x[j] = x[k]
    j = k
  x[j] = t

Алгоритм #2: перестановка блоков

Можно предложить и другой алгоритм, который возникает из рассмотрения задачи с другой точки зрения. Циклический сдвиг массива х сводится фактически к замене ab на bа, где а — первые i элементов х, a b — оставшиеся элементы. Предположим, что а короче b. Разобьем b на b_left и b_right, где b_right содержит i элементов (столько же, сколько и а). Поменяем местами а и b_right, получим b_rightb_leftа. При этом а окажется в конце массива — там, где и полагается. Поэтому можно сосредоточиться на перестановке b_right и b_left. Эта задача сводится к начальной, поэтому алгоритм можно вызывать рекурсивно. Программа, реализующая этот алгоритм, будет достаточно красивой , но она требует аккуратного написания кода, а оценить ее эффективность непросто:

/* Функция swap(a, b, m) меняем местами:
 * x[a..a+m-1] и x[b..b+m-1]
 */
 
if rotdist == 0 || rotdist == n
  exit
 
i = p = rotdist
j = n - p
while i != j
  /* инвариант:
     x[0..p-i] двигать не нужно
     x[p-i..p-1] = a (нужно поменять с b)
     x[p..p+j-1] = b (нужно поменять с a)
     x[p+j..n-1] двигать не нужно */
 
  if i > j
    swap(p-i, p, j)
    i -= j
  else
    swap(p-i, p+j-i, i)
    j -= i
swap(p-i, p, i)

Алгоритм #3: переворотами

Задача кажется сложной, пока вас не осенит озарение («ага!»): итак, нужно преобразовать массив ab в bа. Предположим, что у нас есть функция reverse, переставляющая элементы некоторой части массива в противоположном порядке. В исходном состоянии массив имеет вид ab. Вызвав эту функцию для первой части, получим а^rb (прим. редактора:а^r - это модифицированная часть a, к которой применили фукнцию перестановки reverse). Затем вызовем ее для второй части: получим а^rb^r. Затем вызовем функцию для всего массива, что даст (а^rb^r)^r, а это в точности соответствует bа. Посмотрим, как будет такая функция действовать на массив abcdefgh, который нужно сдвинуть влево на три элемента:

reverse(0, i-1)   /* cba|defgh */
reverse(i, n-1)   /* cba|hgfed */
reverse(0, n-1)   /* defgh|abc */

Дуг Макилрой (Doug Mcllroy) предложил наглядную иллюстрацию циклического сдвига массива из десяти элементов вверх на пять позиций (рис. 2.3); начальное положение: обе руки ладонями к себе, левая над правой: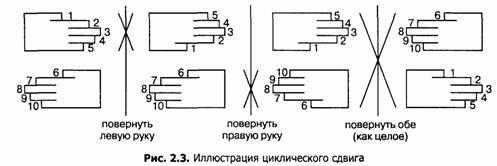

Код, использующий функцию переворота, оказывается эффективным и малотребовательным к памяти, и настолько короток и прост, что при его реализации сложно ошибиться.

Б. Керниган и П. Дж. Плоджер пользовались именно этим методом для перемещения строк в текстовом редакторе в своей книге (В. Kernighan, P. J. Plauger, Software Tools in Pascal, 1981). Керниган пишет, что эта функция заработала правильно с первого же запуска, тогда как их предыдущая версия, использовавшая связный список, содержала несколько ошибок. Этот же код используется в некоторых текстовых редакторах, включая тот, в котором я впервые набрал настоящую главу. Кен Томпсон (Ken Thompson) написал этот редактор с функцией reverse в 1971 году, и он утверждает, что она уже тогда была легендарной.

..."

Реализации:

заполните необходимые поля!

название:
uri-имя*:
заголовок окна:
ЯП:	[другой...] pseudojavajavascriptpythonC++C#CphpGoqbasicrailsrubysmartytsqlvbnetvisualfoxproxmlactionscriptplsqlpascaloracle8sqlvbfortransmalltalkasmcssdelphigroovylispperlmysqlmatlab
код (double click - редактирование) (Esc - предпросмотр)
описание:
автор:	email:
пароль:	[для последующего редактирования]
	подписаться на комментарии**

*	можно кириллицей (недопустимые символы:?&+=\/%#)
**	только для зарегистрированных пользователей

 Циклический сдвиг строки символов, последовательный обмен ссылка |режим:

public void CycleShift(ref String strarr, int rotdist)
{
    int n = strarr.Length;
    for (int i = 0; i < this.GetCommonDivisor(n, rotdist); i++)
    {
        Char t = strarr[i];
        int j = i;
        while (true)
        {
            int k = j + rotdist;
            if (k >= n) k -= n;
            if (k == i) break;
 
            //Делаем strarr[j] = strarr[k];
            this.ReplaceCharInString(ref strarr, j, strarr[k]);
            j = k;
        }
        //Делаем strarr[j] = t;
        this.ReplaceCharInString(ref strarr, j, t);
    }
}

public void CycleShift(ref String strarr, int rotdist) { int n = strarr.Length; for (int i = 0; i < this.GetCommonDivisor(n, rotdist); i++) { Char t = strarr[i]; int j = i; while (true) { int k = j + rotdist; if (k >= n) k -= n; if (k == i) break; //Делаем strarr[j] = strarr[k]; this.ReplaceCharInString(ref strarr, j, strarr[k]); j = k; } //Делаем strarr[j] = t; this.ReplaceCharInString(ref strarr, j, t); } }

Циклический сдвиг массива символов strarr на rotdist позиций

Использует всего несколько дополнительных переменных.

По производительности уступает перестановке блоками и функции переворота

this.GetCommonDivisor() - метод нахождения наибольшего общего делителя
this.ReplaceCharInString() - метод замены символа в строке

Тестировалось на: MS Visual Studio 2005, .NET Framework 2.0

 

 Циклический сдвиг строки символов, перестановка блоков ссылка |режим:

public void CycleShiftByBlocks(ref String strarr, int rotdist)
{
    int n = strarr.Length;
    if (rotdist == 0 || rotdist == n) return;
 
    int i, j, p;
    i = p = rotdist;
    j = n - p;
    while (i != j)
    {
        if (i > j) {
            this.StrSwap(ref strarr, p - i, p, j);
            i -= j;
        } else {
            this.StrSwap(ref strarr, p - i, p + j - i, i);
            j -= i;
        }
    }
    this.StrSwap(ref strarr, p - i, p, i);
}

public void CycleShiftByBlocks(ref String strarr, int rotdist) { int n = strarr.Length; if (rotdist == 0 || rotdist == n) return; int i, j, p; i = p = rotdist; j = n - p; while (i != j) { if (i > j) { this.StrSwap(ref strarr, p - i, p, j); i -= j; } else { this.StrSwap(ref strarr, p - i, p + j - i, i); j -= i; } } this.StrSwap(ref strarr, p - i, p, i); }

Циклический сдвиг массива символов strarr на rotdist позиций перестановкой блоков.

Использует всего несколько дополнительных переменных.
По производительности - наболее быстрый алгоритм среди аналогов.

this.StrSwap() - метод перестановки 2-х отрезков строки

Тестировалось на: MS Visual Studio 2005, .NET Framework 2.0

 

 Циклический сдвиг строки символов, последовательный обмен ссылка |режим:

public void CycleShiftByReverse(ref String strarr, int rotdist)
{
    this.StrReverse(ref strarr, 0, rotdist - 1);
    this.StrReverse(ref strarr, rotdist, strarr.Length - 1);
    this.StrReverse(ref strarr, 0, strarr.Length - 1);
}

public void CycleShiftByReverse(ref String strarr, int rotdist) { this.StrReverse(ref strarr, 0, rotdist - 1); this.StrReverse(ref strarr, rotdist, strarr.Length - 1); this.StrReverse(ref strarr, 0, strarr.Length - 1); }

Циклический сдвиг массива символов strarr на rotdist позиций функцией переворота символов.

Использует всего несколько дополнительных переменных.
По производительности уступает перестановке блоками, но быстрее последовательных обменов

this.StrReverse() - метод переворота символов строки

Тестировалось на: MS Visual Studio 2005, .NET Framework 2.0