Популярные задачи:
Сравнение алгоритмов сортировки массива
- Малые размерности случайных массивов
- Малые размерности частично отсортированных массивов
- Большие размерности случайных массивов
- Большие размерности частично отсортированных массивов
- Выводы
- Все реализации
Зададимся целью исследовать как же поведут себя в реальных задачах сортировки элементарных массивов такие алгоритмы, как: быстрая, пирамидальная, пузырьковая, выбором, вставками, Шелла, Шейкер-сортировка.
Оценивать будем время выполнения, и количество перестановок элементов.
На вход каждой сортировки будем подавать целочисленные массивы с разным количеством элементов: от 10 до 20000.
В 2-х режимах:
- Массивы со случайно сгенерированными числами
- Частично упорядоченные массивы
Помимо этого логично будет проводить 2 вида сравнения:
- На массивах малой размерности(10 - 300 элементов)
- Больших размерностей: 1000 - 20000 элементов
Время будем рассчитывать с точностью до микросекунды. При сравнении на малых размерностях в целях повышения точности время будет отображаться в долях миллисекунды, при больших же размерностях - в долях секунды.
Рассмотрим далее все эти комбинации, погнали!
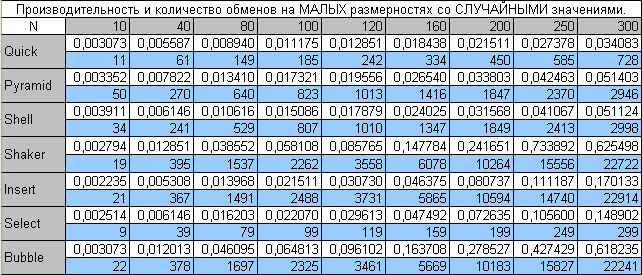
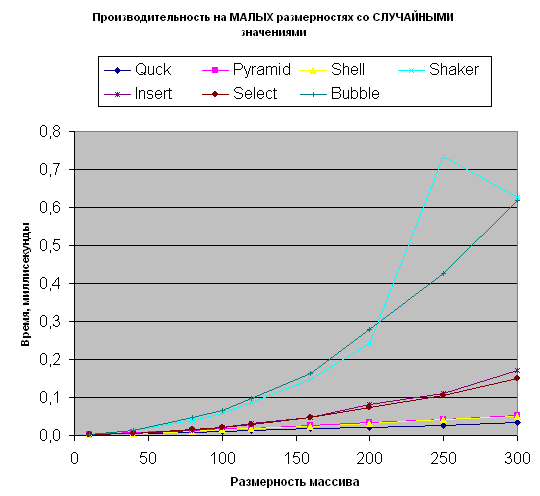
Малые размерности случайных массивов
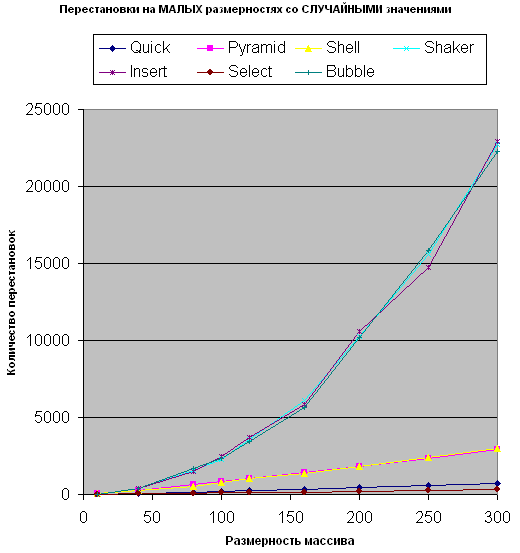
Как видим по скорости лидирует быстрая сортировка. Самые медленные - это пузырьковая и Шейкера.
По количеству перестановок - меньше всего их делает как это ни странно сортировка выбором, затем конечно же быстрая сортировка. Больше всего перестановок делают опять же пузырьковая, Шейкера и Выбором.
Т.о. можно констатировать тот факт, что такие похожие по принципу сортировки алгоритмы как Выбором и Вставками, показывающие почти что одинаковую скорость, радикально отличаются по количеству перестановок: первая(выбором) - делает их меньше чем любой из представленных алгоритмов, вторая(вставками) - наоборот, больше всего.
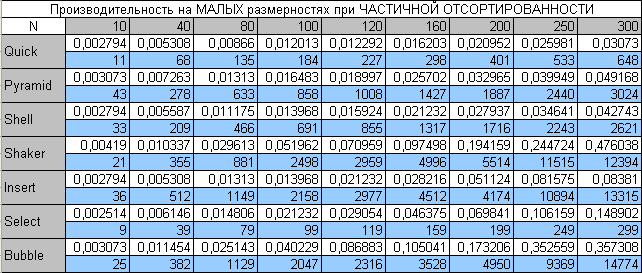
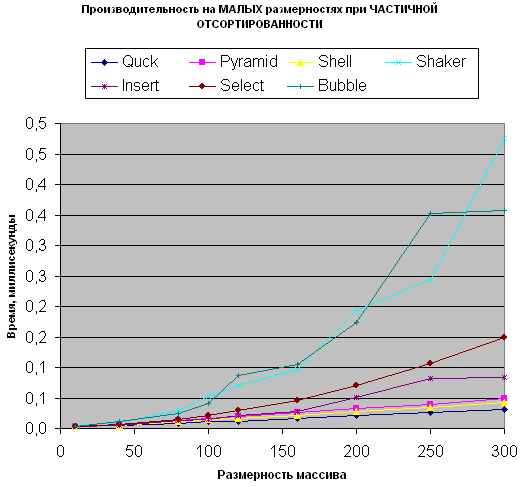
Малые размерности частично отсортированных массивов
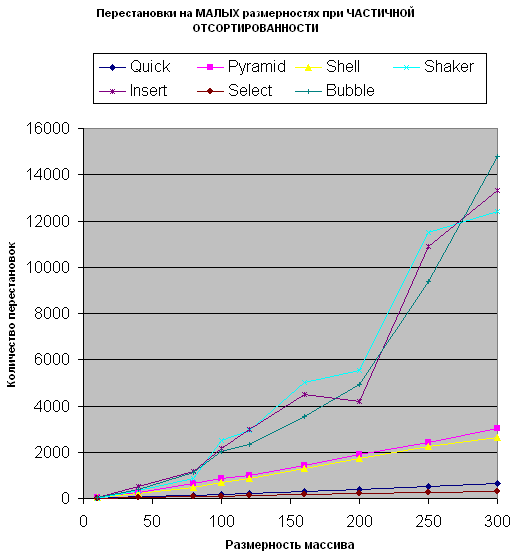
По сравнению с полностью случайными массивами в случае частичной отсортированности на малых размерностях констатируем следующие факты:
- Сортировка вставками начинает опережать сортировку выбором
- Сортировка Шелла начинает опережать пирамидальную и по производительности и по количеству перестановок
- Пузырьковая сортировка делает меньше перестановок чем Вставками и Шейкер
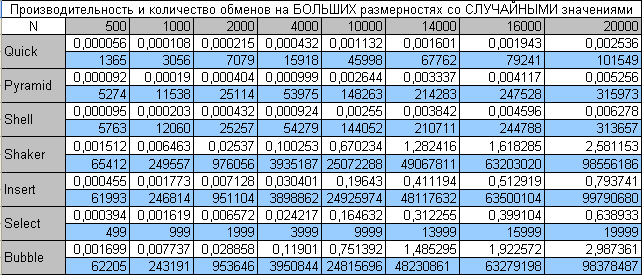
Большие размерности случайных массивов
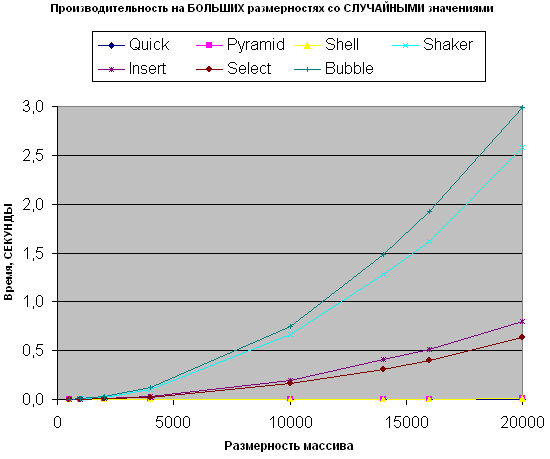
Не видно Быструю, Пирамидальную и сортировку Шелла, поэтому: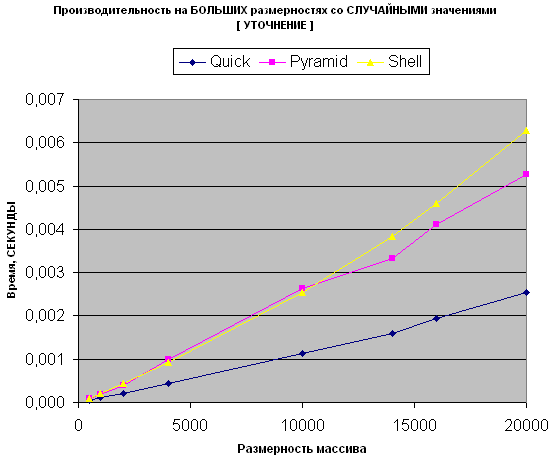
По сравнению со случайными массивами на малых размерностях в случае больших размерностей констатируем следующие факты:
- Шейкер сортировка гарантированно опережает пузырьковую по производительности
- Пирамидальная сортировка примерно после 10 000 -ой размерности начинает опережать Шелла по производительности
- Быстрая сортировка по прежнему остается самой быстрой по производительности и с ростом N только увеличивает это превосходство.
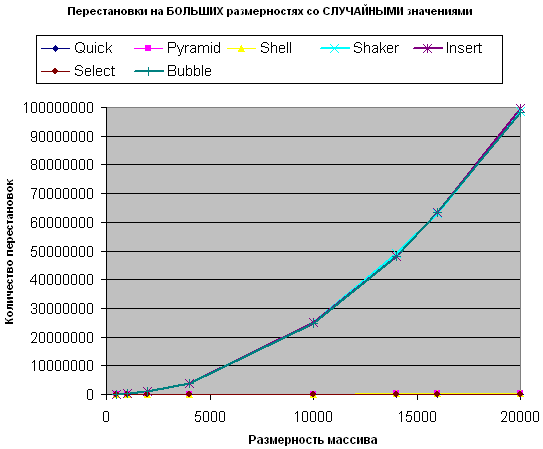
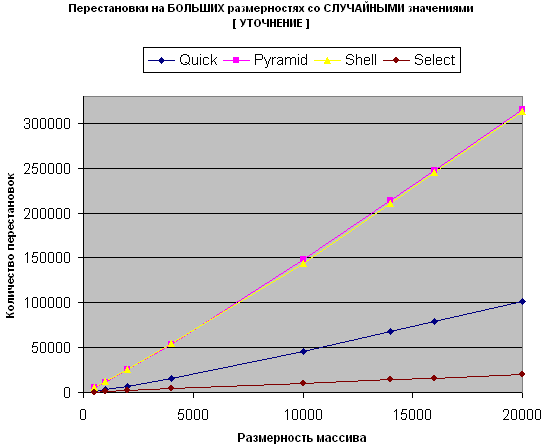
По сравнению с количеством перестановок на малых размерностях - значительных изменений не наблюдается.
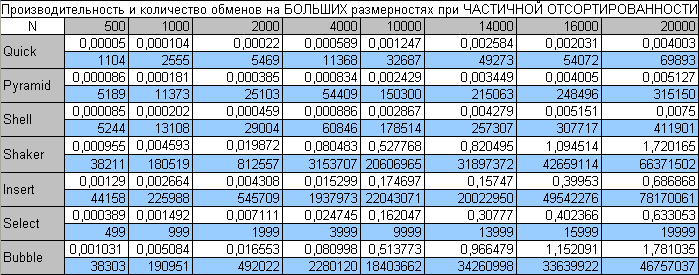
Большие размерности частично отсортированных массивов
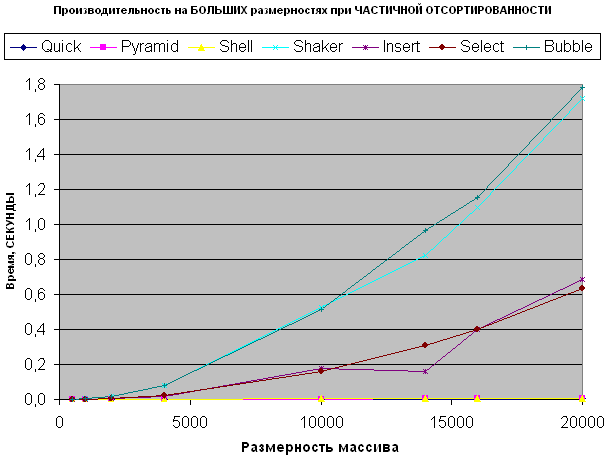
Смотрим что происходит с Пирамидальной, Быстрой и Шелла: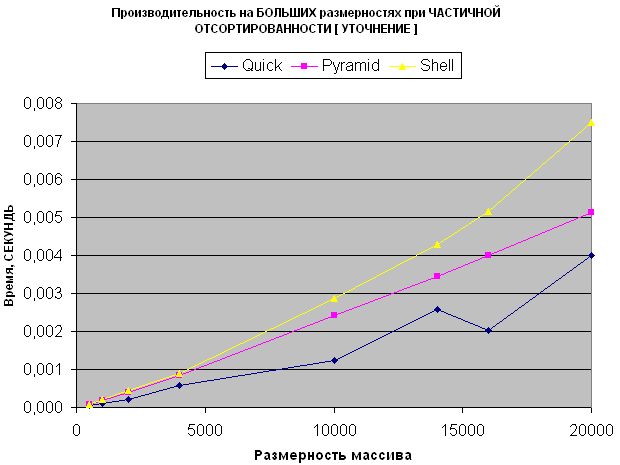
По сравнению с частичной отсортированностью на малых размерностях делаем следующие выводы:
- Шейкер сортировка гарантированно начинает опережать пузырьковую
- Сортировка выбором перестает лидировать над вставками, они начинают показывать примерно одинаковую производительность
- Пирамидальная сортировка теперь уже опережает Шелла на всех значениях
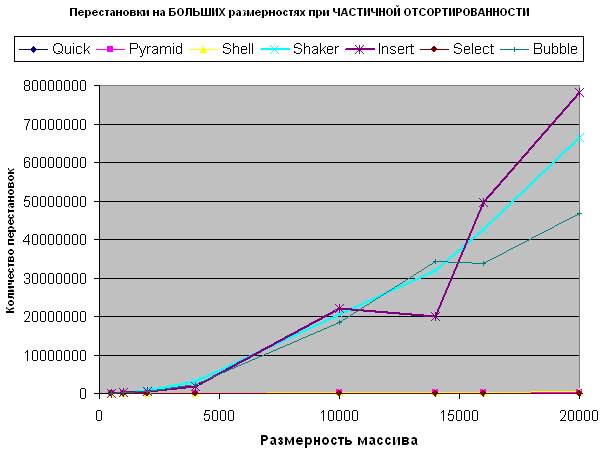
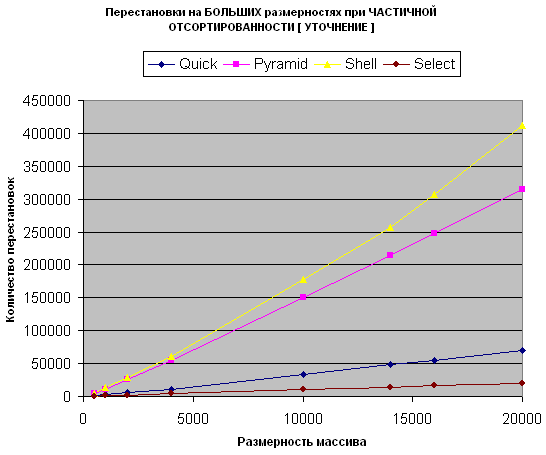
В отличие от перестановок на малых размерностях - здесь пирамидальная сортировка обходит Шелла, делая swap-ов значительно меньше. Лидирует как обычно - сортировка выбором.
Выводы
Быстрая сортировка лидирует по производительности во всех тестах. По количеству перестановок она уступает лишь сортировке Выбором.
Сортировка выбором по производительности в общем случае мало отличается от Вставками, но вот по количеству перестановок - лидирует во всех тестах.
Пирамидальная сортировка и сортировка Шелла: на размерностях ~ больше 10000 пирамидальная быстрей во всех случаях. И лишь на меньших размерностях + в случае случайных значений - сортировка Шелла превосходит пирамидальную.
Шейкер и пузырьковая: первая конечно быстрей, но по количеству перестановок при частичной отсортированности - пузырьковая выигрывает, т.е. делает их меньше.
Реализации:
C++(17) +добавить1) Анализ сортировок: быстрой, пирамидальной, Шелла, Выбором, Вставками, Шейкера, пузырьковой на C++, code #30[автор:this]
2) Sort.h на C++, code #35[автор:this]
3) Sort.cpp на C++, code #36[автор:this]
4) QuickSort.h на C++, code #31[автор:this]
5) QuickSort.cpp на C++, code #32[автор:this]
6) PyramidSort.h на C++, code #33[автор:this]
7) PyramidSort.cpp на C++, code #34[автор:this]
8) ShellSortSedj1.h на C++, code #37[автор:this]
9) ShellSortSedj1.cpp на C++, code #38[автор:this]
10) ShakerSort.h на C++, code #39[автор:this]
11) ShakerSort.cpp на C++, code #40[автор:this]
12) Insert.h на C++, code #41[автор:this]
13) Insert.cpp на C++, code #42[автор:this]
14) Select.h на C++, code #43[автор:this]
15) Select.cpp на C++, code #44[автор:this]
16) BubbleSort.h на C++, code #45[автор:this]
17) BubbleSort.cpp на C++, code #46[автор:this]